What Is Skewed Data: Examples & Types

During peak traffic events, data engineers at streaming platforms like Netflix observe a familiar pattern: 5% of content accounts for 70% of processing load, while most servers sit idle. This computational imbalance—known as data skew—represents one of the most persistent challenges in modern data engineering, where asymmetric distributions can cause distributed systems to fail during critical business moments. Beyond operational headaches, skewed data fundamentally distorts analytical insights, biases machine learning models toward majority classes, and inflates cloud infrastructure costs through inefficient resource utilization.

Skewed data refers to the type of distribution in which the values are not evenly distributed. In distributed computing environments, this asymmetry creates additional challenges where certain partitions or processing nodes handle disproportionately more data than others, leading to system inefficiencies and potential failures. Effectively visualizing the skewed data is crucial as it helps assess the distribution and guides the selection of appropriate transformations.

This article explains all about skewed data, explores how to interpret skewed data, how to measure skewness, and provides comprehensive strategies for managing skew in modern data engineering environments.

What Is Skewness?

Skewness is a statistical measure of asymmetry in a probability distribution around its mean. It indicates whether data points tend to cluster on the left or right side of the mean, with values that can be positive, negative, zero, or undefined.

Skewness is calculated using the third moment of a distribution, standardized by the cube of the standard deviation. This standardization makes skewness values dimensionless and comparable across different datasets regardless of scale or units.

Why skewness matters: Understanding skewness is crucial when working with real-world data, where perfect symmetry is rare. Many classical statistical tests assume normally distributed data, and significant skewness can invalidate these assumptions. This assessment guides your selection of appropriate statistical techniques and determines whether data transformations are necessary.

Practical applications: Skewed data patterns often contain valuable insights beyond being a statistical inconvenience. Power-law distributions in user engagement data reveal platform dynamics, while temporal skew in IoT sensor networks can indicate equipment health patterns. Modern analytical frameworks increasingly use skewness as a feature for predictive modeling rather than just treating it as a preprocessing obstacle.

How Do You Interpret Skewness Values?

Interpreting skewness involves understanding the degree of asymmetry in a probability distribution. Skewness values can vary from negative infinity to positive infinity and provide insights into the distribution's shape. The interpretation of these values helps determine appropriate analytical approaches and identifies potential data quality issues.

Negative Skewness (Left Skewed)

A negative skewness value signifies that the distribution of data points is more on the right side of the curve. Key characteristics include:

• The tail is longer on the left side of the curve and may contain outliers at the lower end
• The mean is typically less than the median
• The bulk of data concentrates toward higher values

Common scenarios: Left-skewed distributions commonly occur in scenarios involving upper bounds or maximum constraints. For example:

• Exam scores when most students perform well, with a few scoring poorly
• Situations where the majority of observations cluster near the higher end of the possible range
• Cases with occasional extreme values pulling the distribution toward the lower end

Data engineering challenges: From a data engineering perspective, negative skewness creates challenges in distributed processing:

• High-value keys dominate the dataset
• Certain processing nodes become overloaded while others remain underutilized
• Requires careful partitioning strategies to prevent imbalances

Advanced solutions: Modern detection techniques now employ:

• Real-time monitoring of partition-level metrics to identify left-skewed workload distributions
• Automated rebalancing algorithms for streaming systems when negative skew patterns emerge
• Dynamic salting strategies that add random prefixes to dominant keys
• Effective spreading of computational work across available resources

Positive Skewness (Right Skewed)

A positive skewness value signifies that the distribution of data points is more on the left side of the curve. Key characteristics include:

• The tail is longer on the right side of the curve with outliers in the upper end
• The mean is often greater than the median
• Most data concentrates toward lower values with occasional extreme high values

Real-world examples: Right-skewed distributions are extremely common in real-world scenarios, particularly in:

• Income distributions
• Website visit durations
• Product sales quantities

This pattern reflects underlying power-law relationships where a small number of entities account for a disproportionate share of the total activity or value.

Technical challenges: In distributed computing environments, positive skewness presents unique challenges:

• A few keys or partitions contain vastly more data than others
• Processing hotspots significantly impact system performance
• Advanced techniques like salting and custom partitioning strategies become essential

Modern cloud solutions: Modern cloud platforms have developed specialized solutions for right-skewed workloads:

• Apache Spark's Adaptive Query Execution automatically detects skewed partitions during shuffle operations
• Dynamic splitting strategies handle imbalanced data distributions
• Automated monitoring tracks partition size ratios
• Configurable thresholds trigger remediation when imbalances exceed 3:1 to 5:1 ratios

Zero Skewness (Symmetric)

A zero-skewness value signifies perfect symmetry of the distribution curve around the mean. Key characteristics include:

• Data points are evenly distributed
• Results in a balanced shape
• The mean, median, and mode coincide
• Creates ideal conditions for many statistical analyses and modeling approaches

Occurrence and importance: Symmetric distributions are relatively rare in natural phenomena but can be:

• Approximated in controlled experimental conditions
• Achieved through data transformation techniques
• Normal distributions represent the most well-known symmetric distribution
• Serve as the foundation for many statistical methods and machine learning algorithms

Computational advantages: From a computational perspective, symmetric data distributions:

• Create optimal conditions for distributed processing
• Naturally balance workloads across processing nodes
• May require preprocessing techniques such as normalization, standardization, or mathematical transformations to achieve

Modern perspective: Contemporary approaches recognize important considerations:

• Forced symmetrization through transformations can eliminate valuable signal in the data
• Modern machine learning frameworks increasingly embrace asymmetric distributions directly
• Specialized algorithms accommodate skewness without requiring normalization:
  
  • Quantile regression
  • Gamma regression
  • Robust estimators

What Are Some Common Examples of Skewed Data?

Let's look into some practical examples of skewed data across different domains and industries, demonstrating how skewness manifests in real-world scenarios and impacts data engineering operations.

Left-Skewed Data Distribution: An example of a left-skewed data distribution is the gestational age of births. Most babies are born full-term, but a few are born prematurely. If we plot the data points, the distribution of values for gestational age of births might look like this, with a longer tail on the left side due to premature births.

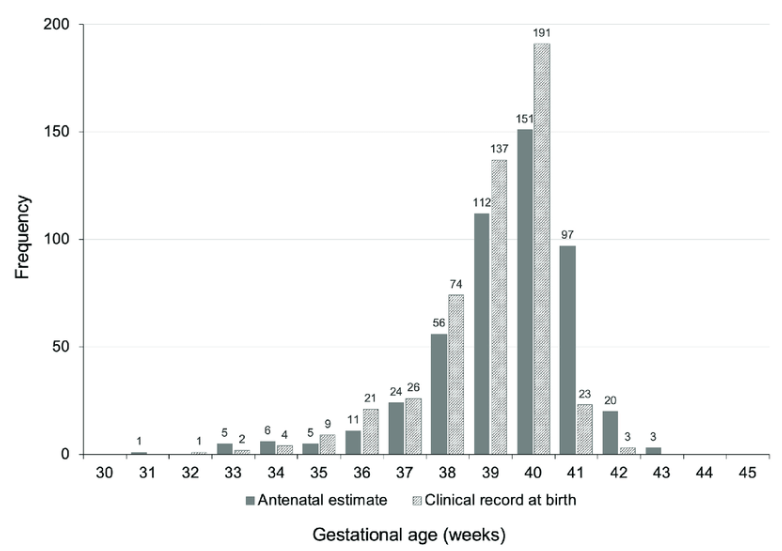
Additional examples of left-skewed distributions include test scores in well-prepared classes, where most students perform well with only a few struggling with the material. Customer satisfaction ratings also frequently exhibit left skewness, as most customers provide positive feedback with fewer extremely negative reviews. These patterns reflect scenarios where there's an upper bound and most observations cluster near that maximum value.

In data engineering contexts, left-skewed distributions often emerge in quality metrics and performance indicators where most systems operate within acceptable ranges but occasional failures create extreme low values. Application response time percentiles, service availability metrics, and data quality scores frequently exhibit this pattern, requiring specialized monitoring approaches that focus on tail behavior rather than central tendencies.

Right-Skewed Data Distribution: An example of a right-skewed data distribution is income distribution in the U.S. Most individuals earn around a moderate income, but a few earn higher incomes. If we plot the data points, the distribution of values for individual incomes might look like the representation below. The high-income earners create a long right tail.

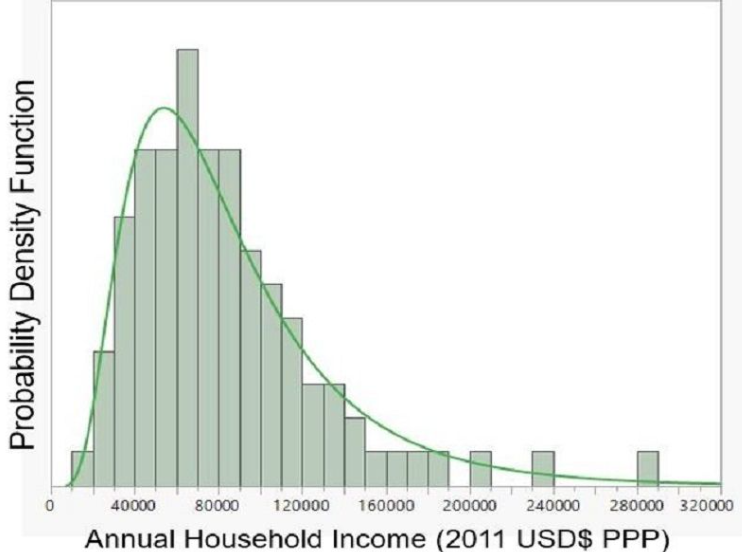
Right-skewed distributions are prevalent in business analytics, including website session durations where most visits are brief but some users spend extensive time browsing. Sales data often exhibits similar patterns, with many small transactions and fewer large purchases. Response times in web applications typically show right skewness, where most requests process quickly but occasional complex operations require significantly more time.

Modern data platforms encounter right skewness in user-generated content systems where a small percentage of creators produce the majority of content. Social media engagement metrics, cloud storage usage patterns, and API request volumes demonstrate similar characteristics. These distributions require specialized handling in distributed systems because traditional hash-based partitioning can create severe load imbalances where a few partitions handle orders of magnitude more data than others.

Zero-Skewed Data Distribution: The height distribution of adults is often symmetrically distributed or zero-skewed since most adults are roughly the same height. For example, the average height of an adult in the U.S. is around 69 inches. If we plot the data points, the distribution of heights might look symmetrical, creating a balanced distribution on both sides of the mean.

Manufacturing quality control metrics often approximate symmetric distributions when processes are well-calibrated and controlled. Temperature readings in stable environments and measurement errors in precise instruments also tend toward symmetrical distributions. These examples demonstrate scenarios where natural variation occurs equally in both directions around a central tendency.

In distributed computing environments, symmetric distributions represent ideal scenarios for load balancing and resource allocation. When data keys distribute symmetrically across hash partitions, processing nodes receive roughly equal workloads, maximizing system efficiency and minimizing latency variability. However, achieving sustained symmetry in real-world data streams often requires active management through preprocessing and partition rebalancing strategies.

Why Is Skewness in Data Important?

Skewness holds significance for various reasons, impacting data analysis and decision-making across multiple domains. Understanding skewness becomes increasingly critical as organizations scale their data operations and implement sophisticated analytics platforms.

Data Preprocessing Guidance – Skewness in datasets guides certain preprocessing strategies. For instance, applying logarithmic or square-root transformations can normalize skewed data, making it more suitable for specific analytical approaches. Modern transformation techniques like Yeo-Johnson extend these capabilities to handle negative values and mixed-sign data common in financial time series and sensor measurements.

Detecting Outliers – Skewness aids in detecting outliers, often indicated by very long tails or large values of the skewness coefficient. Advanced outlier detection now combines skewness analysis with machine learning techniques, using isolation forests and robust estimators to identify anomalous patterns that might indicate data quality issues or genuine extreme events requiring special handling.

Risk Assessment in Finance – Skewness is crucial for assessing investment risks. A highly skewed distribution indicates more volatility, impacting risk management strategies. Financial institutions now employ sophisticated skewness-based models for value-at-risk calculations, stress testing, and regulatory capital requirements that account for tail risks in asymmetric return distributions.

Impact on Measures of Central Tendency – Skewness directly influences the mean, median, and mode. In highly skewed distributions, the median often provides more robust estimates of central tendency than the mean, particularly important for dashboard design and business reporting where misleading averages can distort decision-making processes.

Informed Decision Making – Recognizing skewness enables stakeholders to make more informed decisions by understanding data distribution patterns. Business intelligence systems increasingly incorporate skewness awareness into automated alerting and anomaly detection, helping analysts identify when underlying data patterns change significantly from historical baselines.

Impact on Statistical Tests – Many parametric tests assume normality. Skewness assessment determines whether transformations or alternative tests are necessary. Modern statistical software automatically tests for skewness and recommends appropriate non-parametric alternatives when distributional assumptions are violated.

Performance Optimization in Distributed Systems – In data engineering contexts, skewness significantly impacts system performance and resource utilization. Contemporary cloud platforms implement skew-aware scaling and load balancing to prevent hotspots that can degrade entire cluster performance during peak processing periods.

How Do You Measure Skewness?

The measures of skewness quantify the asymmetry of a probability distribution. Common approaches include several well-established mathematical methods, each with specific use cases and interpretive frameworks. Modern computational tools have automated these calculations while extending traditional methods with robust alternatives for large-scale data analysis.

1. Karl Pearson's Coefficient of Skewness

Pearson's first skewness coefficient (mode skewness)  

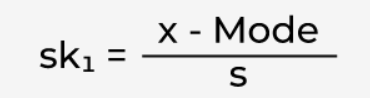
Pearson's second skewness coefficient (median skewness)  

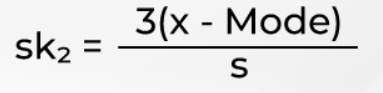
Interpretation:  

Pearson's coefficients remain foundational but exhibit sensitivity to outliers that can distort skewness estimates in real-world datasets. Modern implementations often combine these classical measures with robust alternatives to provide more reliable skewness assessment in the presence of extreme values or data quality issues.

2. Kelly's Measure

Interpretation:  

Kelly's measure provides valuable insights particularly for grouped data and frequency distributions. This approach proves especially useful in data engineering contexts where exact values may not be available but frequency counts within ranges can be efficiently computed across distributed systems.

3. Bowley's Measure

Interpretation:  

Bowley's measure offers robustness advantages because it relies on quartiles rather than moments, making it less sensitive to extreme values. This characteristic makes it particularly valuable for streaming data analysis where outliers or data quality issues might temporarily affect moment-based calculations.

Contemporary skewness measurement incorporates additional robust techniques including the medcouple, which provides enhanced outlier resistance, and machine learning-based distribution fitting that can handle multimodal or complex distributional patterns that traditional measures might mischaracterize.

What Are Advanced Detection and Mitigation Strategies for Skewed Data?

Modern data engineering environments require sophisticated approaches to detect and mitigate skewed data beyond traditional statistical measures. These strategies encompass both computational and analytical frameworks designed to handle skew across distributed systems and complex data pipelines.

1. Computational Skew Detection in Distributed Systems

Real-time monitoring capabilities: Modern systems integrate comprehensive telemetry that provides:

• Partition-level tracking of data distribution patterns across cluster nodes
• Statistical process control techniques for establishing dynamic thresholds
• Automatic alerts when partition size ratios exceed acceptable bounds

Key metrics monitored:

• Shuffle read sizes
• Task execution times
• Memory pressure
• Identifies skewed workloads before they cause system failures

Predictive detection approaches: Modern distributed computing frameworks implement sophisticated metrics collection for predictive capabilities:

• Analysis of historical patterns in data distribution
• Correlation with operational metrics like garbage collection frequency and spill-to-disk events
• Machine learning models trained on system telemetry data
• Prediction of partition imbalances with sufficient lead time for corrective measures

Dynamic resource allocation: Systems respond to detected skew through intelligent resource redistribution:

• Allocates additional memory and CPU resources to nodes handling skewed partitions
• Scales back resources on underutilized nodes
• Elastic cloud platforms: Automatically provision additional compute instances when skew patterns exceed cluster capacity

2. AI-Driven Skew Management

Predictive prevention techniques: Contemporary skew management leverages AI to prevent issues before they impact performance:

• Unsupervised learning: Analyzes data ingestion patterns to identify emerging skew conditions
• Detection algorithms: Isolation forests and one-class support vector machines flag anomalous patterns
• Learning capabilities: Models understand normal distribution characteristics and trigger alerts for significantly different skew profiles

Supervised learning applications: Models trained on historical skew incidents provide early warning capabilities:

Key features analyzed:

• Partition size variance during ingestion
• Changing value distributions in partition keys
• Correlations between data source updates and processing delays

Performance: When trained on sufficient historical data, these models achieve high accuracy in identifying skew conditions 30-60 minutes before system bottlenecks occur.

Reinforcement learning optimization: Advanced systems use reinforcement learning to optimize partitioning strategies:

• Experiments with various partition key combinations, salting strategies, and data bucketing approaches
• Measures impact on system performance continuously
• Develops sophisticated policies adapting partitioning strategies based on observed patterns
• Continuously improves load balancing effectiveness over time

3. Partitioning and Load Balancing Strategies

Hash-based partitioning with salting: A fundamental technique for distributing skewed keys across multiple partitions:

• Dynamic salting: Adjusts salt ranges based on observed key frequencies
• Smart distribution: Highly popular keys get distributed across more partitions than less common ones
• Adaptive maintenance: Systems maintain metadata about key frequency distributions and automatically adjust strategies as usage patterns evolve

Range-based partitioning: Particularly effective for specific data types:

Optimal use cases:

• Time-series data
• Naturally ordered datasets where temporal patterns create predictable skew

Advanced implementations:

• Adaptive range boundaries that adjust based on observed data density
• Prevention of hotspots from specific time periods or value ranges with disproportionate data
• Analysis of historical load patterns to predict optimal range boundaries for future periods

Machine learning-driven partitioning: Custom algorithms learn optimal distribution strategies from operational data:

• Multi-technique approach: Combines multiple partitioning techniques
• Intelligent selection: Uses decision trees or neural networks to select appropriate strategies for specific data characteristics
• Continuous adaptation: Adapts strategies based on system performance monitoring feedback‍
• Superior performance: Achieves better load balancing than static partitioning schemes

How Does Federated Learning Address Label Distribution Skew?

Federated learning systems face unique skewed data challenges because training data remains distributed across client devices and organizations, often exhibiting significant heterogeneity in both feature distributions and label patterns. Traditional centralized approaches to skew mitigation cannot be directly applied due to privacy constraints and the decentralized nature of federated architectures.

Logits Calibration for Non-IID Label Distributions

Core breakthrough approach: Federated Learning via Logits Calibration represents a breakthrough for handling scenarios where different clients have vastly different class distributions in their local datasets.

Real-world application: This technique addresses situations common in healthcare applications:

• Different hospitals may specialize in treating different types of patients
• Results in dramatically skewed label distributions across participating institutions
• Creates significant challenges for traditional federated learning approaches

Technical implementation process: The calibration process involves sophisticated coordination:

Client-side operations:

• Clients compute class-specific margins during local training
• Margins compensate for their local label distribution bias
• Calculations based on local class frequencies
• Margins transmitted alongside model updates to central aggregation server

Server-side processing:

• Server computes global margin adjustments
• Helps rebalance learning signals across all participating clients
• Prevents clients with heavily skewed class distributions from dominating the global model

Implementation requirements:

• Careful coordination between client-side training processes and server-side aggregation algorithms
• Clients maintain privacy-preserving statistics about local class distributions
• Server develops robust aggregation strategies accounting for varying levels of class imbalance

Performance benefits: This approach has demonstrated significant improvements in minority class performance without compromising overall model accuracy.

Dynamic Weighting and Data Valuation Techniques

Advanced client weighting systems: Modern federated learning systems implement dynamic client weighting based on sophisticated assessment criteria:

• Uses data distribution similarity rather than simple dataset size metrics
• Employs density estimation techniques to assess alignment with desired global distribution
• Assigns higher weights to clients whose local data is more representative of the overall population

Privacy-preserving distribution assessment: Masked Autoencoder for Density Estimation enables secure evaluation:

• Clients train lightweight autoencoder networks on their local data
• Share only the learned distribution parameters with the central server
• Raw data never exposed during the assessment process

Server-side similarity computation:

• Server computes similarity metrics between client distributions
• Adjusts aggregation weights to emphasize contributions from clients with more balanced data
• Prioritizes clients with representative data distributions

Adaptive learning mechanisms: Adaptive aggregation algorithms provide continuous improvement:

Dynamic weight adjustment factors:

• Current data characteristics analysis
• Historical contribution quality assessment
• Performance impact tracking on validation datasets

Feedback-driven optimization:

• Systems track how different clients' contributions affect global model performance
• Uses feedback to refine weighting strategies over time
• Clients with consistent global model improvements receive higher weights
• Clients with consistently skewed contributions are automatically down-weighted

Collaborative Model Training Approaches

Multi-stage training methodology: Advanced systems separate skew correction from core model optimization:

Stage 1 - Pattern Discovery:

• Focuses on identifying and characterizing skew patterns across the federated network
• Establishes baseline understanding of distribution imbalances

Stage 2 - Targeted Correction:

• Implements correction strategies based on discovered patterns
• Allows systems to address distribution imbalances without compromising learning efficiency

Hierarchical federated learning architecture: Sophisticated grouping strategies optimize training effectiveness:

Client grouping approach:

• Groups clients with similar data distributions
• Performs intermediate aggregation within each group
• Conducts final global aggregation across groups

Benefits achieved:

• Reduces impact of extremely skewed clients on the global model
• Preserves benefits of diversity in training data
• Clients with similar class distributions train together in sub-federations
• Results aggregated at higher level to create final global model

Privacy-preserving validation systems: Advanced assessment mechanisms maintain strict privacy standards:

Secure performance evaluation:

• Enables assessment of global model performance across different client distributions
• Never exposes sensitive local data during evaluation
• Uses secure aggregation protocols to compute performance metrics on federated validation sets
• Maintains strict privacy guarantees throughout the process

Adaptive training optimization: Validation results inform sophisticated adaptive strategies:

• Adjusts learning rates based on observed performance patterns
• Modifies aggregation weights for different client types
• Optimizes training schedules based on client-specific performance data
• Enables continuous improvement of federated learning effectiveness

What Are Real-Time Skew Detection Techniques in Stream Processing?

Stream processing systems face unique skewed data challenges because data distributions can change rapidly and unpredictably, requiring real-time detection and mitigation strategies that operate within strict latency constraints. Traditional batch-oriented skew detection methods fail to address the dynamic nature of streaming data where skew patterns can emerge and disappear within seconds.

AI-Driven Anomaly Detection for Streaming Skew

Adaptive Skew Scoring systems: Advanced systems use online machine learning algorithms for continuous real-time assessment:

Feature extraction capabilities:

• Partition sizes monitoring
• Record arrival rates tracking
• Key cardinality metrics analysis
• Real-time streaming data pattern recognition

Machine learning integration:

• Feeds extracted features into unsupervised learning models
• Flags anomalous distribution patterns as they emerge
• Provides continuous assessment of partition balance and data distribution patterns

Isolation Forest algorithms for streaming: Specialized adaptations provide efficient anomaly detection:

• Minimal overhead: Identifies skewed partitions with minimal computational cost
• Lightweight architecture: Maintains decision trees that partition feature space of normal distribution patterns
• Rapid identification: Quickly identifies data points falling outside expected ranges
• Automated response: Triggers automated skew mitigation procedures when partition metrics exceed learned normal boundaries

Exponential smoothing techniques: Advanced temporal analysis provides predictive capabilities:

• Trend tracking: Tracks temporal trends in skew patterns over time
• Predictive modeling: Enables prediction of skew probability based on recent distribution history
• Running estimates: Maintains estimates of partition balance metrics continuously
• Deviation detection: Detects when current observations deviate significantly from predicted values
• Robust early warning: Combination of trend analysis with anomaly detection provides comprehensive early warning systems

Dynamic Resource Allocation and Auto-scaling

Skew-aware autoscaling systems: Modern systems integrate sophisticated distribution-aware scaling:

• Beyond throughput: Moves beyond simple throughput-based scaling to consider data distribution patterns
• Real-time calculation: Calculates partition skew ratios in real-time
• Configurable thresholds: Triggers scaling decisions when imbalances exceed thresholds (typically 3:1 to 5:1 ratios)
• System tolerance: Threshold settings depend on individual system tolerance levels

Kubernetes-based streaming platforms: Advanced container orchestration for streaming workloads:

Custom metrics implementation:

• Implements custom metrics exposing partition-level load information
• Integrates with horizontal pod autoscalers for intelligent scaling decisions

Automated resource provisioning:

• Automatic detection: When skew detection systems identify imbalanced partitions
• Dynamic provisioning: Automatically provisions additional processing pods
• Workload redistribution: Redistributes workloads using consistent hashing or dynamic partition assignment strategies
• Resource optimization: Ensures skewed workloads receive additional resources without over-provisioning entire cluster

Spot instance orchestration: Cost-effective cloud resource management:

• Transient resources: Leverages cloud provider's transient compute resources specifically for skewed partitions
• Rapid scaling: Quickly spins up additional compute capacity when skew is detected
• Backlog processing: Uses additional resources to process backlogged data from overloaded partitions
• Automatic cleanup: Once skew condition resolves, temporary resources are automatically released
• Cost optimization: Optimizes cost while maintaining performance standards

Real-Time Mitigation Strategies

Dynamic salting systems: Intelligent salt generation for real-time adaptation:

Advanced salting approach:

• Real-time adjustment: Adjusts salt generation strategies based on observed key frequency patterns
• Beyond static methods: Unlike static salting with fixed random prefixes
• Proportional distribution: Generates salt values proportional to key frequency
• Optimal distribution: Ensures most popular keys get distributed across the most partitions
• Continuous updates: Salt pools are updated continuously as key popularity patterns evolve

Stateful stream processing frameworks: Sophisticated key redistribution without interruption:

• Live redistribution: Implements key redistribution strategies that move hot keys between processing nodes
• No downtime: Operates without stopping the entire stream
• State migration: Maintains state migration capabilities for relocating specific key processing
• Load balancing: Moves keys to less loaded nodes while preserving processing guarantees
• Consistency maintenance: Preserves exactly-once processing guarantees and state consistency

Backpressure control systems: Intelligent flow control for skew management:

Selective flow control:

• Skew-aware implementation: Implements skew-aware flow control with selective capabilities
• Partition-specific: Can selectively slow down data ingestion for specific partitions
• Balanced processing: Maintains normal processing rates for balanced partitions
• System protection: Prevents skewed partitions from overwhelming the system
• Unaffected performance: Allows unaffected partitions to continue processing at full speed

Advanced coordination:

• Multi-stage coordination: Advanced implementations coordinate backpressure across multiple pipeline stages
• Cascading prevention: Prevents cascading slowdowns throughout the system
• Comprehensive protection: Provides system-wide protection while maintaining optimal performance

How Can Airbyte Help You Address Skewness in the Data?

Airbyte provides comprehensive solutions for managing skewed data throughout the entire data integration lifecycle, from source extraction through destination loading and transformation processes. The platform's architecture specifically addresses skew-related challenges that commonly emerge in modern data pipelines.

600+ Pre-Built Connectors with Skew-Aware Design – Airbyte's extensive connector library incorporates intelligent data extraction strategies that automatically handle skewed source systems. Database connectors implement Change Data Capture with incremental synchronization that prevents large batch operations from creating processing bottlenecks. API connectors include rate limiting and pagination strategies specifically designed to handle endpoints with uneven response sizes and varying data volumes.

Advanced Change Data Capture Optimization – The platform's CDC capabilities intelligently manage skewed update patterns by monitoring table modification frequencies and adjusting sync strategies accordingly. Tables with heavy write activity receive more frequent incremental updates with smaller batch sizes, while rarely modified tables use larger, less frequent synchronization windows. This adaptive approach prevents skewed write patterns from overwhelming destination systems.

Kubernetes-Native Scaling for Skewed Workloads – Airbyte's cloud-native architecture automatically scales processing resources based on actual workload characteristics rather than simple throughput metrics. The platform monitors partition sizes, processing times, and memory utilization patterns to identify skewed sync operations and automatically allocate additional resources to prevent pipeline failures during periods of uneven data distribution.

Intelligent Destination Optimization – The platform provides destination-specific optimizations for major cloud data warehouses that handle skewed data patterns efficiently. For Snowflake destinations, Airbyte implements cluster key optimization and automatic table clustering that maintain query performance even with highly skewed fact tables. BigQuery integration includes partition strategy optimization that prevents hotspots in time-partitioned tables with uneven temporal distributions.

Real-Time Transformation and Normalization – Through deep integration with dbt, Airbyte enables real-time application of skewness correction transformations including logarithmic scaling, Box-Cox transformations, and quantile normalization. These transformations can be applied automatically as data flows through the pipeline, ensuring downstream analytics systems receive properly normalized data without requiring separate preprocessing steps.

Comprehensive Observability and Monitoring – Airbyte provides detailed monitoring of partition sizes, processing times, and resource utilization patterns that enable proactive skew detection. The platform's observability features include configurable alerting for skewed processing patterns and integration with popular monitoring platforms for comprehensive pipeline health assessment. Teams can establish custom alerts for partition imbalance conditions and automated responses to common skew scenarios.

Enterprise Security and Governance – For organizations managing skewed sensitive data, Airbyte provides comprehensive PII masking and data protection capabilities that maintain statistical properties while ensuring compliance. The platform's role-based access controls and audit logging help organizations manage access to skewed datasets that may contain concentrated sensitive information.

What Are the Key Considerations for Skewed Data Management?

Understanding the multifaceted implications of skewed data requires examining statistical, computational, and business dimensions that intersect in modern data systems. Effective skew management strategies must address these interconnected concerns while maintaining system reliability and analytical accuracy.

Statistical Considerations

The choice between mean and median as measures of central tendency becomes critical when working with skewed distributions, as the mean can be heavily influenced by extreme values while the median provides more robust estimates of typical values. In business reporting contexts, this distinction affects dashboard design and KPI calculations where misleading averages could lead to poor decision-making.

Variability measures also require careful selection in skewed data contexts, as standard deviation can be inflated by extreme values while interquartile range provides more stable estimates of spread. Modern analytics platforms increasingly provide both parametric and non-parametric measures automatically, allowing users to select appropriate statistics based on detected skewness levels.

Ensuring analytical methods remain valid under skew conditions requires understanding the robustness properties of different statistical techniques. Linear regression assumptions can be severely violated by skewed residuals, while tree-based methods often handle skewness naturally. Contemporary machine learning frameworks increasingly incorporate automatic skewness testing and recommend appropriate algorithms based on detected data characteristics.

Computational Performance Impact

Memory allocation strategies must account for skewed data patterns that can create uneven resource consumption across processing nodes. In distributed systems, a few partitions with skewed data may require significantly more memory than others, leading to out-of-memory errors even when total cluster memory appears adequate. Modern resource management systems implement dynamic allocation that adjusts memory quotas based on observed partition characteristics.

CPU utilization patterns in skewed workloads often exhibit high variance across cluster nodes, with some processors being fully utilized while others remain idle. This imbalance reduces overall system efficiency and increases processing time for the entire workload. Advanced scheduling algorithms now consider data distribution patterns when assigning tasks to processing nodes to maximize resource utilization.

Network bottlenecks frequently emerge in skewed data processing when certain nodes must transfer or receive disproportionate amounts of data during shuffle operations. Modern distributed systems implement adaptive network management that can prioritize traffic from overloaded nodes and implement compression strategies specifically optimized for skewed data patterns.

Business Decision-Making Implications

Dashboard design for skewed metrics requires careful consideration of visualization techniques that accurately represent asymmetric distributions without misleading business users. Traditional bar charts and line graphs may not effectively communicate the presence of extreme values, while box plots and histogram overlays provide better insight into distribution characteristics. Modern business intelligence platforms increasingly provide automatic skewness detection that suggests appropriate visualization approaches.

Forecasting models that accommodate asymmetric distributions require specialized techniques beyond traditional time series methods that assume symmetric error distributions. Quantile regression, gamma regression, and other approaches specifically designed for skewed data can provide more accurate predictions and better uncertainty estimates for business planning purposes.

Risk assessment frameworks must account for skewed distributions in financial and operational metrics, as traditional normal distribution assumptions can severely underestimate tail risks. Modern risk management systems incorporate heavy-tailed distributions and extreme value theory to provide more robust risk estimates that account for asymmetric loss patterns commonly observed in business operations.

Conclusion

Handling skewed data represents a fundamental challenge that spans statistical analysis, computational optimization, and business intelligence in modern data systems. The evolution from simple transformation techniques to sophisticated AI-driven detection and mitigation strategies reflects the growing complexity of data environments where skew can emerge at multiple levels from individual features to distributed system architectures.

Contemporary approaches to skewed data management emphasize proactive detection through real-time monitoring, predictive analytics, and automated response systems that can adapt to changing data patterns without human intervention. The integration of federated learning techniques for handling label distribution skew and real-time stream processing capabilities for dynamic skew mitigation represents significant advances beyond traditional batch-oriented methods.

Organizations that successfully implement comprehensive skew management strategies combining statistical rigor with computational optimization achieve better analytical accuracy, improved system performance, and more reliable business insights. By leveraging platforms like Airbyte that provide built-in skew handling capabilities alongside advanced detection and monitoring tools, data engineering teams can focus on creating business value rather than managing infrastructure bottlenecks caused by asymmetric data distributions.

The future of skewed data management lies in increasingly autonomous systems that can predict, detect, and mitigate skew conditions across the entire data lifecycle while preserving the informational value contained within asymmetric patterns. As data volumes continue to grow and distribution patterns become more complex, these advanced skew management capabilities will become essential for maintaining competitive advantage in data-driven organizations.

Frequently Asked Questions

What impact does data skew have on machine learning model performance?

Data skew significantly impacts machine learning models by creating imbalanced training distributions that can lead to biased predictions. Models trained on skewed datasets often exhibit poor performance on minority classes or underrepresented value ranges. For classification tasks, this manifests as reduced precision and recall for less frequent classes. In regression problems, skewed data can cause models to underestimate extreme values and produce higher prediction errors in tail regions.

Modern approaches to address this include specialized sampling techniques like SMOTE for classification tasks, weighted loss functions that emphasize minority classes, and ensemble methods that combine multiple models trained on different data distributions. Transfer learning techniques can also help by leveraging knowledge from more balanced domains when the target domain exhibits severe skew.

How can I determine if my data transformation has effectively addressed skewness?

Evaluating transformation effectiveness requires both statistical assessment and practical validation. Start by calculating skewness coefficients before and after transformation, aiming for values closer to zero post-transformation. Visual inspection using Q-Q plots can reveal whether the transformed data better approximates a normal distribution.

Beyond statistical measures, evaluate practical effectiveness by examining the performance of downstream processes. For machine learning applications, compare model performance metrics on transformed versus untransformed data. For distributed computing, measure resource utilization balance and processing times across partitions. Effective transformations should improve both statistical properties and practical outcomes in your specific use case.

What are the trade-offs between addressing skewness and preserving original data characteristics?

Balancing skew correction against data fidelity involves significant trade-offs. Transformations that reduce skewness (like logarithmic or power transformations) can improve statistical model assumptions but may alter the interpretability of results. For instance, coefficient interpretations become less intuitive after log transformations.

Additionally, aggressive skew correction can eliminate meaningful signal in the data, particularly when skewness represents natural phenomena rather than data quality issues. Domain knowledge becomes crucial in determining whether skewness represents valuable information or problematic distortion. Modern approaches increasingly favor techniques that accommodate skewness within models rather than forcing symmetry through transformations, preserving the original data characteristics while handling the statistical challenges.

How does skew handling differ between batch and streaming data processing systems?

Batch and streaming systems require fundamentally different approaches to skew management. Batch systems can analyze complete datasets before processing, enabling global optimization strategies like pre-computed partitioning schemes, custom shuffle algorithms, and data transformations applied before main processing begins.

Streaming systems must detect and mitigate skew in real-time without complete dataset knowledge. This requires dynamic techniques including adaptive partitioning that adjusts as distribution patterns emerge, continuous monitoring systems that track partition health metrics, and backpressure mechanisms that prevent overwhelmed partitions from causing system-wide failures. Additionally, streaming systems often implement stateful skew correction that maintains historical distribution information to predict and prevent recurring skew patterns. These real-time approaches necessarily trade some optimization precision for processing immediacy.

‍